Modeling healthcare costs is often problematic because they are abnormally distributed. There are typically a large number of $0 observations (i.e., people who do not use any health care services) and a strongly right-skewed distribution of costs among health care users due to a disproportionate number of people with very high health care costs. This observation is well known to health economists, but a complicating factor for modelers is mapping the cost of disease to specific health care states. For example, while the cost of cancer care can vary depending on the stage of the disease and whether the cancer has progressed; The cost of cardiovascular disease will be different if the patient suffers a myocardial infarction.
an article of Zhou et al. (2023) provides a good tutorial on how to estimate costs with disease model states using generalized linear models. The tutorial contains the main steps.
Step 1: Prepare the data set:
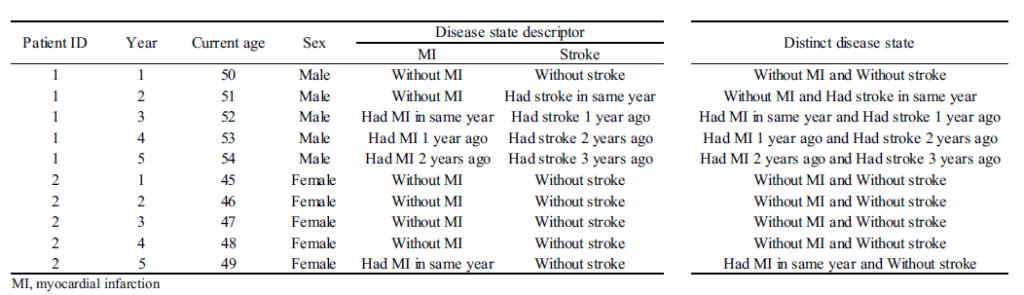
- The data set typically requires calculating the cost for discrete time periods. For example, if you have claims data, you may have cost information by date, but for analytical purposes you may want to have a data set with cost information per person (rows) whose columns represent cost by year ( or month). Alternatively, you could create the unit of observation to be person-year (or person-month) and each row would be a separate person-year record.
- Next, the pathological states must be specified. In each time period, the person is assigned a disease state. Challenges include determining how granular the states should be (e.g., MI only vs. time since MI) and how to handle multiple state scenarios.
- When data are censored, one can (i) add a covariate to indicate that the data is censored or (ii) exclude observations with partial data. If cost data are missing (but the patient is not censored), multiple imputation methods can be used. To form the analysis time periods it is necessary to map the cycle length of the decision model, handle censoring appropriately, and potentially transform the data.
- Below is a sample data set.
Step 2: Model Selection:
- The article recommends using a two-part model with a generalized linear model (GLM) framework, as OLS assumptions about normality and homoscedasticity in residuals are often violated.
- With the GLM, the expected value of the cost is transformed nonlinearly, as shown in the following formula. You must estimate both a link function and the distribution of the error term. “The most popular (link and distribution function combinations) for healthcare costs are linear regression (identity link with Gaussian distribution) and gamma regression with a natural logarithm link).
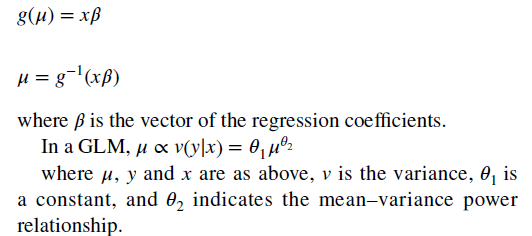
- To combine the GLM with a two-part model, one simply estimates the above equation at all positive values and then calculates a logit or probit model for the probability that an individual has a positive cost.
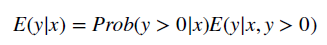
Step 3: Select the final model.
- Model selection must first consider which covariates are included in the regression which can be obtained by stepwise selection using a prespecified statistical significance. However, this can result in over-tightening. Alternative covariate selection techniques include bootstrap selection and penalized techniques (e.g., minimum angle selection and shrinkage operator, LASSO). Interactions between covariates could also be considered.
- The overall fit can be evaluated using the mean error, the mean absolute error, and the mean squared error (the latter being the most commonly used). Better fitting models have smaller errors.
Step 4: Model prediction
- While it is easy to predict costs, the impact of disease status on costs is more complex. The authors recommend the following:
For a one-part nonlinear model or a two-part model, marginal effects can be derived using recycled prediction. It includes the following two steps: (1) run two scenarios in the target population setting the disease state of interest to be (a) present (e.g., recurrent cancer) or (b) absent (e.g., no cancer recurrence). ); (2) calculate the difference in average costs between the two scenarios. The standard errors of the difference in means can be estimated using bootstrapping.
The authors also provide an illustrative example of the application of this approach to model hospital costs associated with cardiovascular events in the United Kingdom. The authors also provide sample code in R and you can download it. here.








